Objectif : Réalisation d'un marégraphe à partir d'une vidéo basse résolution et à l'aide d'un réseau de neurones ( CNN : Convolution Neuronal Network )
Les caméras étant placées devant les échelles de marée, le problème se résume à trouver un algorithme efficace permattant d'évaluer automatiquement le niveau de la mer à partir des échelles de marée. Les études menées auparavant par le laboratoire LIENSs de La Rochelle et ses partenaires ont abordé ce problème par des méthodes classiques de traitement d'images (traitement sur les contrastes, seuillages, niveaux d'histogrammes ...) qui ont abouti à des resultats peu satisfaisants. En effet, les conditions météorologiques perturbent la lecture des images. De plus la faible résolution de l'image, 1 à 1.2 pixels par cm, limite la précision de la hauteur estimée.
Nous avons travaillé à partir de 980 images d'échelles de mareé anotées manuellement, ce qui nous a permis d'envisager une solution de segmentation utilisant les réseaux de neurones artificiels. Le réseau apprend à identifier les caractéristiques (appellées features), à partir desquelles une prédiction est proposée. Pour la segmentation, le réseau génère un tableau de probabilités de la taille de l'image qui détermine à quelle classe appartiennent les pixels ( classe 1, le pixel fait partie de l'echelle, classe 0 le pixel n'appartient pas à l'echelle). Un réseau de convolution (CNN : convolution neuronal network) a été utilisé, la structure convolutive permettant d’extraire des caractéristiques de l’image grâce à une succession de filtres appelés noyaux de convolutions, transformant l’image initiale en un ensemble d’images appelées cartes de convolution.
Réseau de neurones :
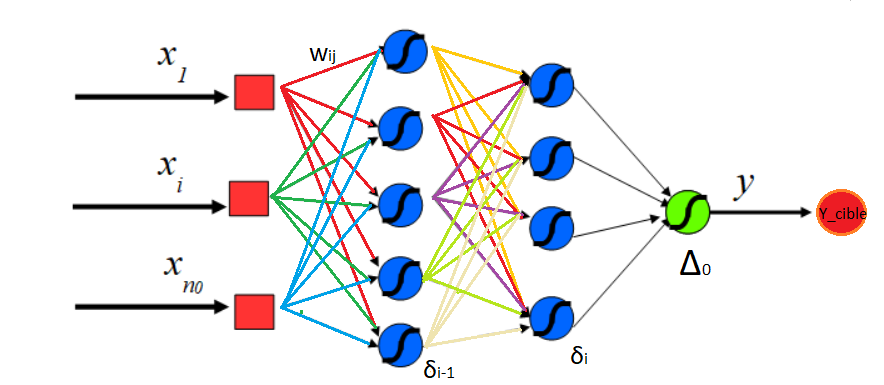
La phase apprentissage s'effectue par une minimisation itérative de la fonction de coût choisie grâce à une descente de gradient. La fonction de coût permet d'évaluer une distance entre la valeur prédite par le modèle et la valeur réel. Cette dernière dépend des poids $w_{ij}$ ainsi que des valeurs de prédictions $y_i$.
Pour un réseau (fcn : full conneted network voir le schéma ci dessous) le calcul de la valeur d'activation est la somme $a(x) = f(\sum w_i x_i + b)$ où $f$ est la fonction d'activation. Les $x_i$ sont les valeurs d'entrée des neurones,les $w_i$ sont les poids qui sont ajustés au cours du processus d'apprentissage, les $b_i$ sont les valeurs de biais et les $a_i$ sont les valeurs d'activation de chaque neurone d'une couche donnée.
La mise à jour des poids s'écrit : $w_i = w_{i+1} - \eta \Delta L$ soit $\Delta w_i = - \eta \Delta L$, avec $\eta$ le taux d'apprentissage et $L$ la fonctions de coût (Loss function).
En ce qui concerne les réseaux convolutionnels, les valeurs d'activation pour une couche $l$ sont $x^{l}{ij}= f(\sum _m \sum _n w^{l}} x^{l-1{i+m,j+n} + b^{l})$.
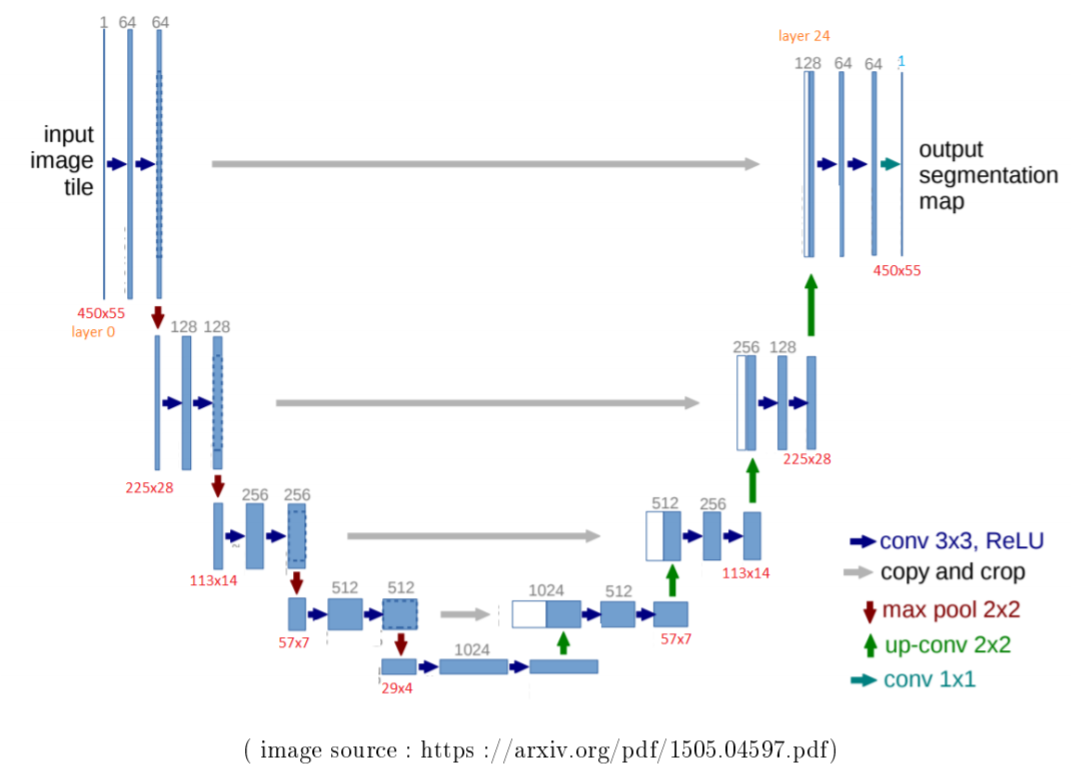
Pour la segmentation, nous avons opté pour un réseau U-net
La fonction de coût choisie est la cross entropie. La distance à minimiser est donnée par :
$d(y_{prediction}y_{cible})= - \sum_i y_{cible_i}log(y_{prediction_i})$
L'initialisation du réseau nécessite la réalisation de calques qui sont des images binaires :

Les résultats
L'algorithme a été testé sur les 980 images dont 200 seulement ont servi pour l'entraînement (le réseau n'étant pas pré-entrainé). Les résultats fournis par cette méthode sont très bons comparés à ceux obtenus auparavant. L'erreur moyenne est de 3.5 cm pour la lecture du niveau de la mer. Les images ci-dessous montrent le résultats de la segmentation de quelques images pour lesquelles le détourage de l'échelle est effectué automatiquement grâce aux filtres obtenus par l'inférence.

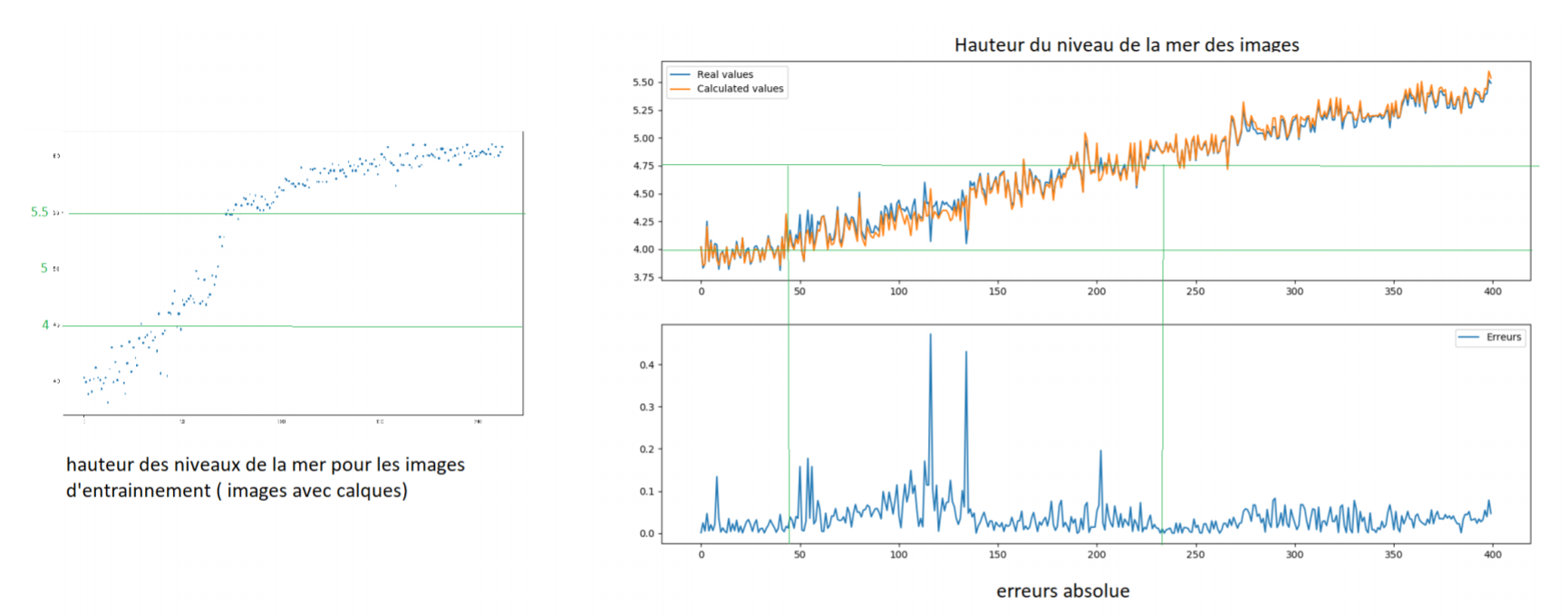
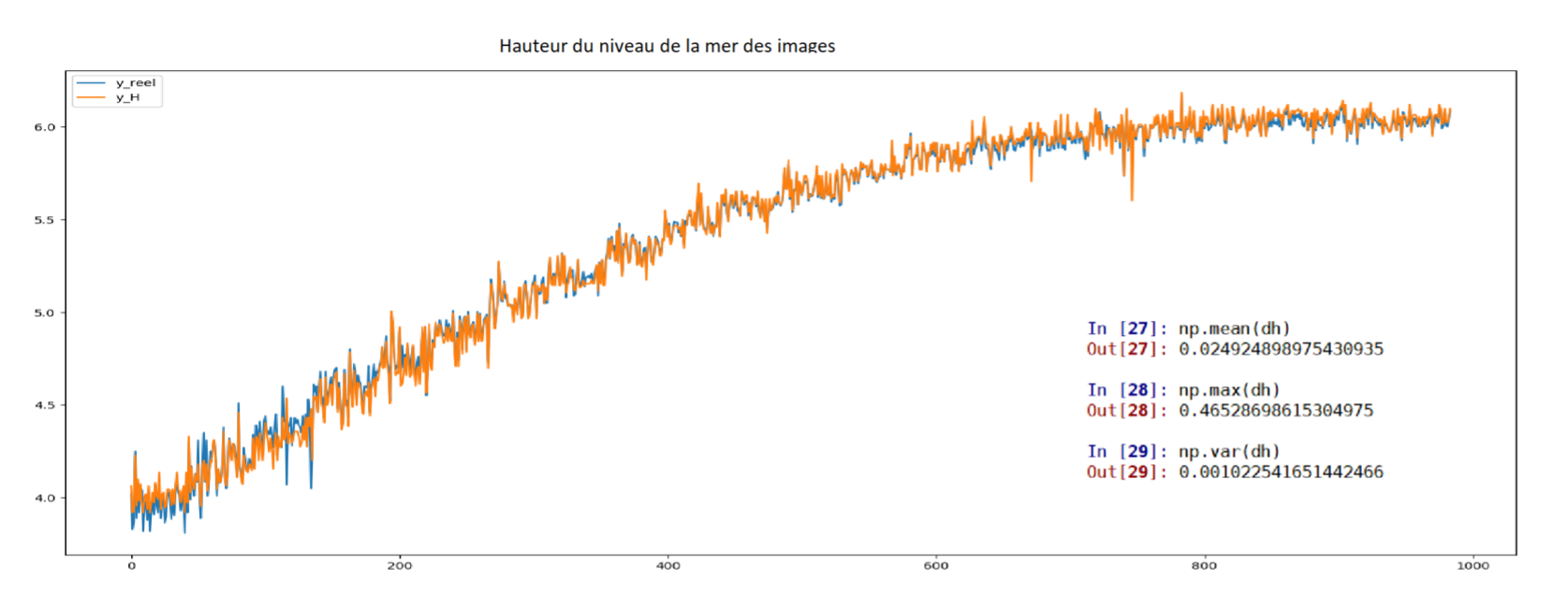
Un traitement par homographie et une normalisation des données par batchs (lot de données traitées en même temps) ont permis d'améliorer l'erreur moyenne pour obtenir 2.5 cm, comme le montre le graphique ci-dessous.
On peut observer que la zone où il y a eu le moins d'images d'entrainement a un taux d'erreur plus élevé. Ce qui illustre le fait que plus il y a de données, meilleure est la prédiction.
Conclusion :
Ce travail montre bien la pertinence des approches Deep Learning dès que l'on dispose d'une base de données suffisante pour l'apprentissage. Dans notre cas, 200 images seulement ont été utilisées. Compte tenu de la résolution, l'erreur moyenne obtenue de 2,5 cm, après traitement par homographies, parait quasi-optimale. Un travail supplémentaire permettrait éventuellement de réduire le temps d'apprentissage à l'aide par exemples d'un réseau pré-entrainé ou une architecture RCNN.