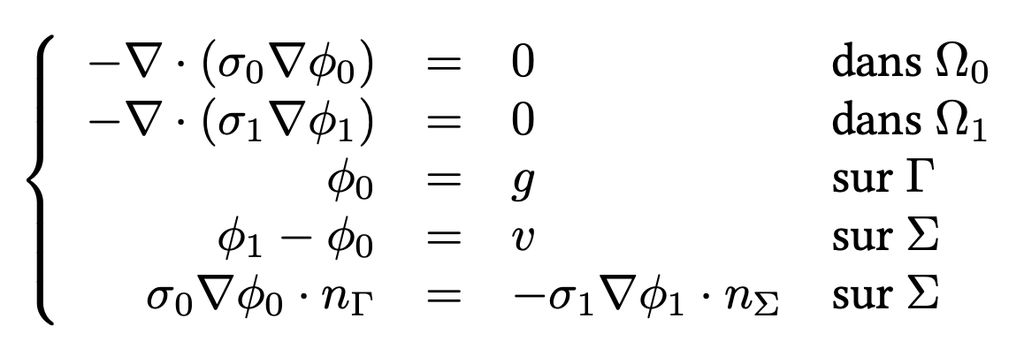Présentation
Nos diplômés sont des experts hautement qualifiés en Intelligence Artificielle, en Modélisation et Simulation, pour l’industrie et la recherche. Le Master mention Mathématiques et Applications, parcours Mathématiques et Interactions MIX, de La Rochelle Université forment des étudiants capables de modéliser et/ou simuler une situation concrète ou théorique afin de résoudre un problème, capables également de mettre en œuvre des méthodes des mathématiques numériques afin de proposer une solution concrète tout en sachant s'assurer de la pertinence des résultats fournis par la méthode. Les diplômés du Master MIX ont des compétences d’ingénieurs mathématiciens qui leur permettent d’envisager soit une insertion professionnelle en entreprise, soit une insertion professionnelle dans des laboratoires de recherche via des contrats doctoraux. Le Master MIX est une formation innovante confrontant l’expertise scientifique académique aux problématiques des entreprises et des pouvoirs publics. C’est avant tout à partir de ces problématiques que sont appréhendés les fondamentaux en mathématiques et mathématiques appliquées.
À l’issue de sa formation, un étudiant est capable :
- D’appréhender une problématique en termes d’ingénierie : il aide, en le formulant mathématiquement, à clarifier un problème et à mettre en évidence les principaux obstacles, et ce conformément aux objectifs applicatifs définis en accord avec ses partenaires.
- D’exploiter des données sources : il extrait des informations fiables et exploitables contenues dans de grands volumes de données (numériques) produits par diverses modalités d’acquisition.
- De représenter et visualiser l’information : il représente les éléments d’information pertinents pour l’élaboration de modèles sous forme exploitable par ses collaborateurs.
- De construire et/ou d’adapter un modèle cohérent : il développe et met en œuvre des techniques mathématiques efficientes, robustes, mais avant tout fiables, en vue de simulations réalistes.
- De valider et de restituer l’information : il restitue après validation les réponses apportées au problème initial et ce sous forme exploitable par ses collaborateurs.
Maîtrisant ainsi l’ensemble de la démarche, en particulier les contributions théoriques les plus récentes des mathématiques, le diplômé MIX apporte un gage de qualité et de fiabilité aux réponses apportées. Compte tenu des objets d’étude propres à la formation, un étudiant diplômé de MIX possède des compétences spécifiques très pointues relevant :
- De la modélisation discrète et continue.
- Des équations de conservation et des modèles de diffusion.
- Des méthodes numériques.
- Du traitement et de l’analyse du signal et des images.
- Des mathématiques du Machine Learning et de l’Intelligence Artificielle.
Le Cursus
S1
Majeure :
- PDE Analysis
- Programming tools and methods
- Signal and image processing
Mineure :
- Machine learning and artificial intelligence (Beginners)
Transversal :
- Anglais, Mathématiques et R&D, Séminaire junior
S2
Majeure :
- Modeling, analysis and simulation
- Numerical methods
- Optimization and random dynamics
Mineure :
- Machine learning and artificial intelligence (Advanced)
Transversal :
- Anglais, Mathématiques et R&D, Séminaire junior
S3
Majeure :
- Advanced tools and methods for signal and image processing
- Geometry for science
- Deep learning
Mineure :
- Machine learning and artifical intelligence (Practical approach)
Transversal :
- Anglais, Mathématiques et R&D,, Séminaire junior
S4
Stage en laboratoire ou en entreprise.
La maquette et la présentation officielle du Master MiX est sur le site de La Rochelle Université.
Les semaines Mathématiques et Entreprises
Les ECs Mathématiques et R&D des semestres 1 et 3 sont consacrés à des semaines « Mathématiques et entreprises ». Ces dernières sont organisées sous la forme d'un défi à relever. La semaine débute par une présentation de l'entreprise ou de l'organisme, avec éventuellement une visite sur site. Un problème concret de R et D est soumis aux étudiants qui ont une semaine pour apporter une réponse pertinente concrète et exploitable par l'entreprise. L'équipe encadrante est mobilisée pendant toute la semaine pour accompagner les recherches des étudiants. À la fin de la semaine, ces derniers organisent une séance de restitution des résultats obtenus devant les responsables ayant soumis le problème.
Quelques exemples :
- Débruitage d’images échographiques avec l’entreprise ECM (Angoulême)
- Analyse automatique d’une partie filmée de Backgammon avec la Fédération Française de Backgammon
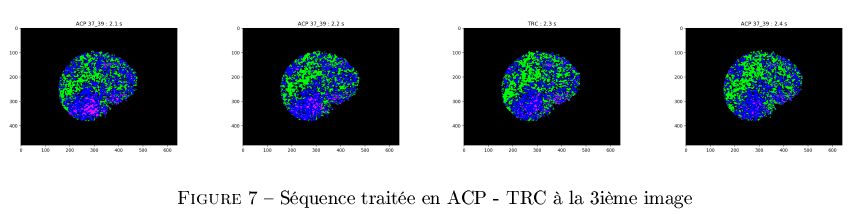
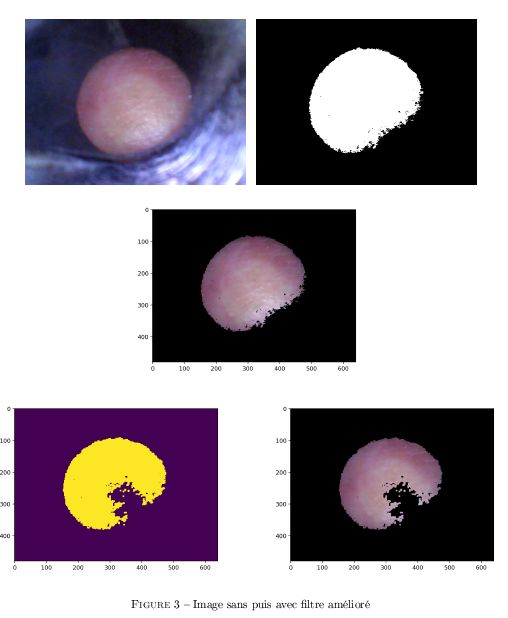
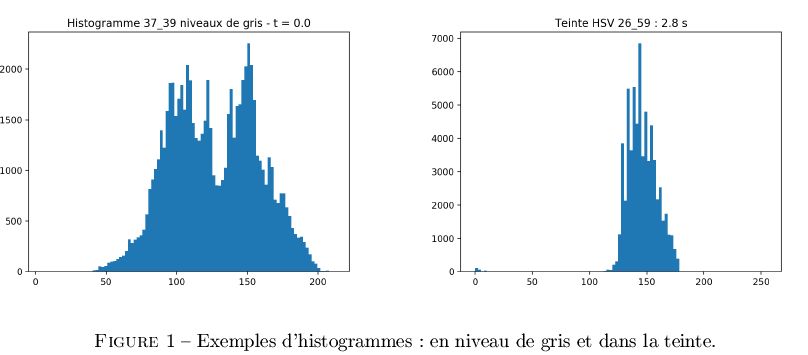
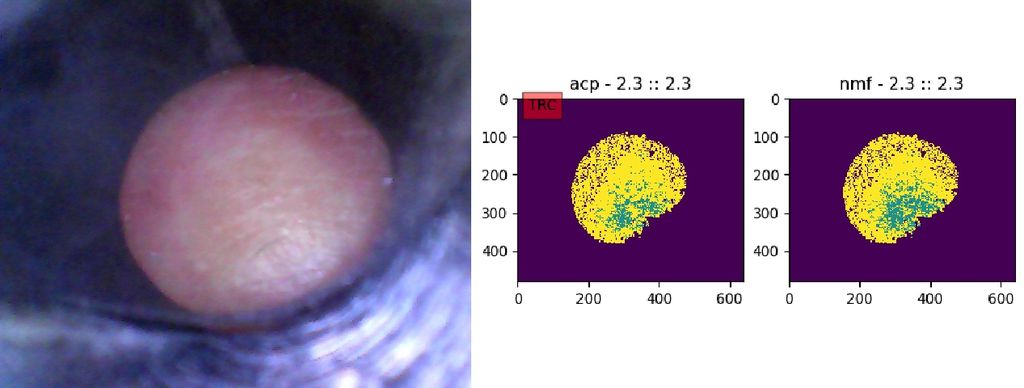
- Détection du temps de recoloration cutanée avec la Start-Up DICARTECH (Annonay)
- Analyse de signaux EEG pour le Neurofeedback avec la Start-Up ULLO (La Rochelle)
- Détection et suivi de cathéters avec l’IHU LYRIC (Bordeaux)
- Analyse de la configuration de voiles à partir de vidéos avec l’entreprise MADINTEC (La Rochelle)
- Analyse de feuilles d’émargement avec l’entreprise EXPERT-SOLUTIONS et l’IRTSNA (Bordeaux)
- Recalage de nuages de points 3D avec l’entreprise CARBON AXIS (La Rochelle)
- Détermination de la bathymétrie à partir de la position des crêtes de vagues avec le laboratoire LIENSS (La Rochelle)
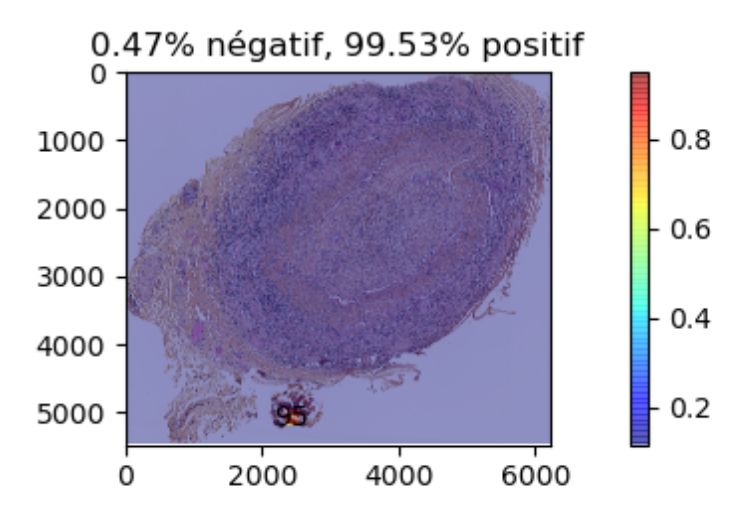
- Aide au diagnostic de la maladie de Horton à partir d’images anapath avec le Centre Hospitalier La Rochelle
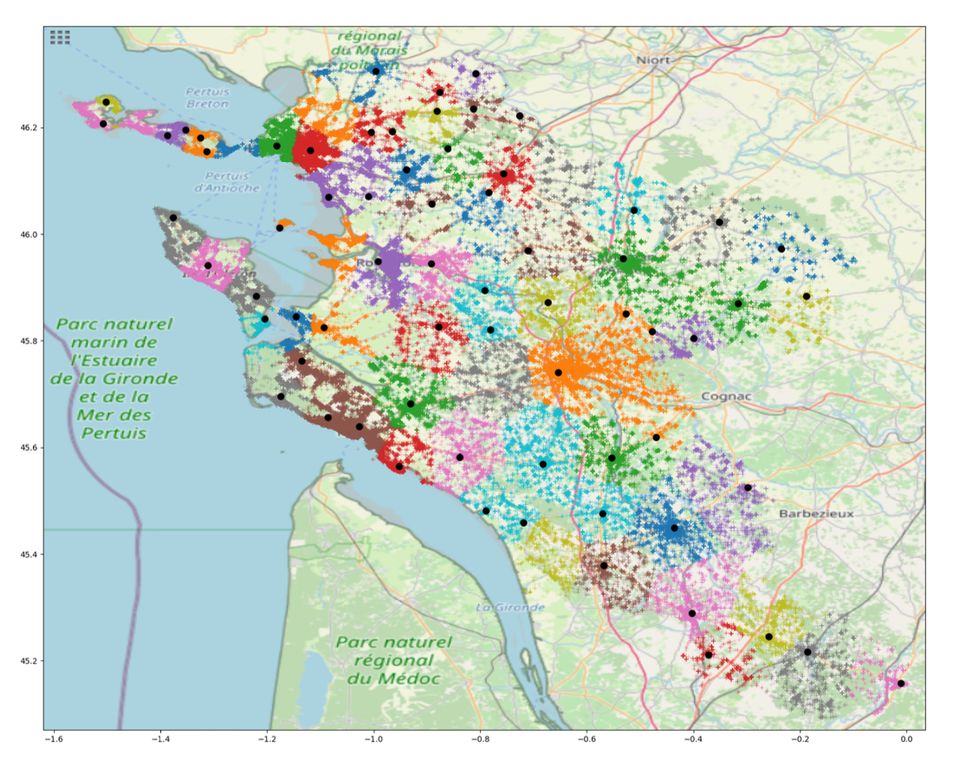
- Optimisation de la répartition géographique des casernes de pompiers avec le SDIS 17.
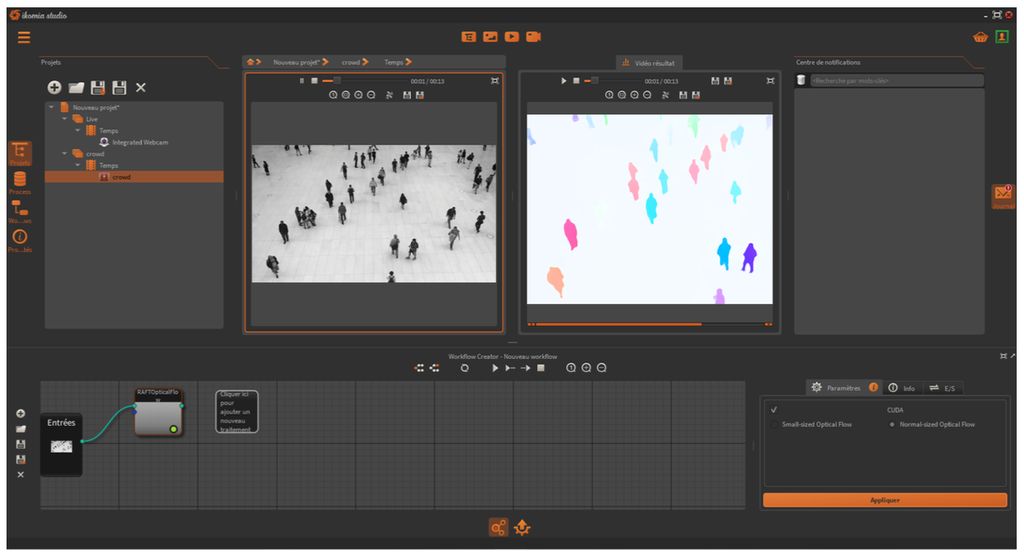
- Détection précoce de feux à partir de captations vidéos et d’algorithmes d’IA, avec le SDIS17.
- Estimation de la hauteur d’eau lors d’inondations à partir d’images de drones et d’algorithmes d’IA, avec le SDIS17
- Analyse par images satellites de la dynamique d’eutrophisation, applications au lac d’aydat, avec INRAE
- Reconnaissance automatique de larves de bivalves marins à partir d’images de microscopie, avec CAPENA
- Caractériser génétiquement des espèces de moules à partir de leur caractéristiques morphologiques, avec IFREMER
- Détection d’endofuites de type II à l’aide d’algorithme de Deep Learning, avec l’hôpital de La Rochelle
Les Séminaires juniors
Ces ECs ont pour objectif d’initier les étudiants à la recherche. Des intervenants, le plus souvent des collaborateurs des chercheurs du laboratoire MIA, leur présentent des travaux très actuels et des problématiques ouvertes. Le travail demandé est un travail de synthèse comprenant un état de l’art, un résumé argumenté des exposés, le cas échéant des précisions sur les points abordés, ou encore des codes Python illustratifs. Les étudiants sont également chargés de rédiger des supports de communication comme des articles en anglais avec un format Latex imposé ou des présentations au format Beamer. L’équipe pédagogique veille à cet égard à ce que les étudiants respectent les principes de déontologie et d’éthique liés à la production de ces supports.
Quelques exemples :
- Mathématiques et perception des couleurs, E. Provenzi, Bordeaux
- COVID-19: mathematical modelling, optimal control and complex network of a SAIRP model, C. Silva, Aveiro
- Modelling of energy storage in porous media: From CO2 or hydrogen to thermochemical heat storage, R. Helmig, Stuttgart
- Unsupervised Deep Learning Algorithm for PDE-based Forward and Inverse Problems, N. Sochen, Tel Aviv…
Stages de semestre 2 :
Quelques exemples
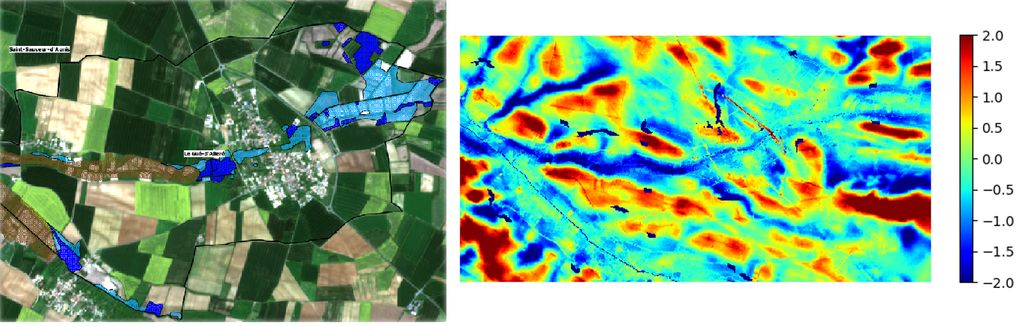
- Analyse d'image satellite pour la pré-localisation des zones humides (UNIMA, La Rochelle)
- Suivi des anticorps pour le cancer du côlon (INRIA Bordeaux)
- Développement d'un logiciel de gestion de la mesure (CASPEO, Orléans)
- Prix du crédit carbone (ATLANTECH, La Rochelle) - Réalisation d'un marégraphe à partir d'une vidéo basse résolution et à l'aide d'un réseau de neurones (Laboratoire LIENSS, La Rochelle)
- Définition et mise en œuvre d’une méthode d’assimilation de données (SEE-D, Vannes)
- Améliorations statistiques de prévisions atmosphériques en un point (NUMTECH, Clermont-Ferrand)
- Étude des propriétés mécaniques de fibres de lin, relation structure-comportement par approche numérique (INRAE Nantes)
- Algorithme de supervision automatisé et détection de comportements suspects (Vrai + Local, La Rochelle)…
- Numerical modeling of the flash sintering process: cyclic nature of the current pulses inducing heating (TENSYL)
- Détermination objective d’audiogramme à partir des mesures de potentiels évoqués auditifs (Institut Pasteur)
- Coupling waves, nearshore processes, groundwater flow and saline dispersion in a coastal aquifer (Lab. Geosciences Montpellier and Beach Institute GLADYS)
Stages de semestre 4 :
Quelques exemples
- Apprentissage automatique des paramètres d’un effet de réverbération audio 3D (B<>COM, Rennes)
- Prédiction du niveau de pauvreté par Deep Learning à partir d’une séquence d’images satellite (LIRMM, Montpellier)
- Modélisation numérique microscopique de la propagation des potentiels d’action cardiaques (INRIA, Bordeaux)
- Segmentation du spectre de fouillis de mer pour la détection de petites cibles mobiles (BOWEN, Saclay)
- Phénotypage à haut débit de cultures associées par Deep Learning (INRA, Toulouse)
- Modélisation de la résistance bactérienne. Étude de l’impact des rejets d’antibiotiques dans l’environnement (GRETHA, Bordeaux)
- Analyse et implémentation d’algorithmes de référence pour la détection d’objets et la segmentation sur données satellitaires (IKOMIA, La Rochelle)
- Estimation des incertitudes des données et des prédictions d’un modèle profond pour la classification d’emboles cérébraux par doppler transcrânien (CREATIS, Lyon)
- Mise en place d’une méthode de Pricing (SEE-D, Vannes).
- Advanced Generative Models for Synthetic Mobility Data: A Novel Application of Denoising Diffusion GANs to Trajectory Generation (ORANGE)
- Sky Polarization for Determining Earth’s Geographic North: Application to Automobile Navigation (STELLANTIS)
- Modelling and numerical simulation of active slender structures (MAP5)
- Near Infrared using Transfer Learning (STMicroelectronics)
- Classification des sous-types de cancer de la vessie, ICONE : Images, Clinical and Omics data in GAT with Node and Edge features (INRIA et Institut Curie)
- Embedded 3D Object Detection for Autonomous Driving using both Image and Point Cloud modalities (CEA)
Les savoirs
-
Apprentissage Machine et Intelligence Artificielle. La thématique est abordée des points de vue théorique, algorithmique , et de mise en applications. Les fondements mathématiques concernent aussi bien l’algèbre linéaire, les probabilités et les statistiques, que l’optimisation ou encore la modélisation géométrique ou physique. La maîtrise des outils et méthodes mathématiques permet d’assurer la pertinence de la mise oeuvre d’algorithmes via Python, Tensorflow, Pytorch… On s’intéresse également aux grandes familles modernes de réseaux : MLP, CNN, VAE, LSTM, RNN, GAN, Transformers et LLM, ainsi qu’à la méthodologie de production de datasets dans divers contextes (données textuelles, séries temporelles, images au sens large, par exemple satellitaires ou médicales, vidéos…). Un focus particulier est fait sur les questions de robustesse, de reproductibilité, d'explicabilité ou encore de frugalité.
-
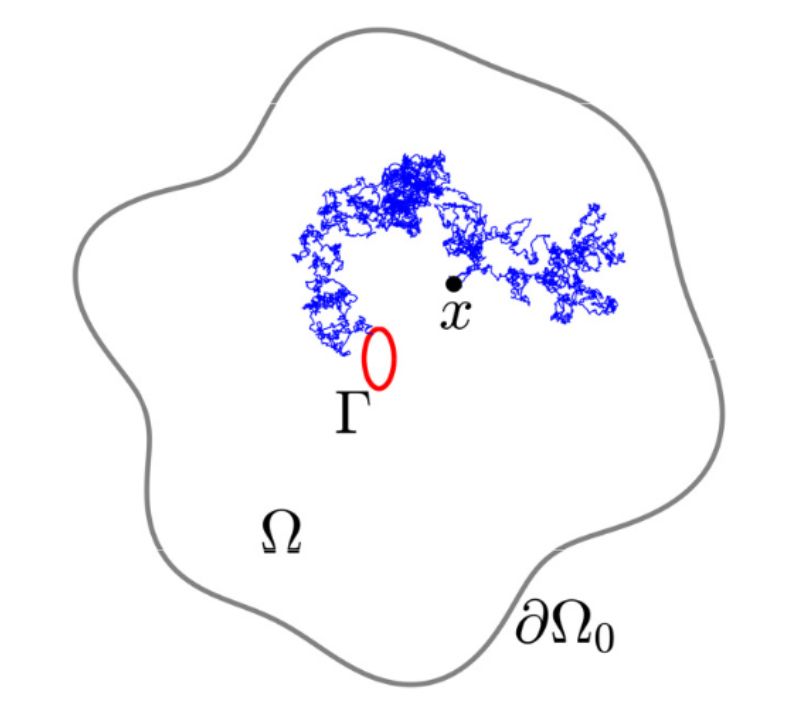
Modélisation discrète et continue. Il s’agit ici de comprendre les liens entre les processus microscopiques ou mésoscopiques et les phénomènes observés à l’échelle humaine. Les notions importantes sont donc celles d’échelles, ou d’espace-échelle, et de résolution. L’étude des processus microscopiques est par nature discrète : on s’intéresse à des déplacements de particules (modélisés par des marches aléatoires). Celle des phénomènes effectifs est par nature continue, relevant par exemple de la mécanique des fluides (modélisée par des équations de conservation). La compréhension des échelles pertinentes et des couplages entre ces échelles est primordiale. L’étape finale consiste à passer à l’échelle de la prédiction.
-
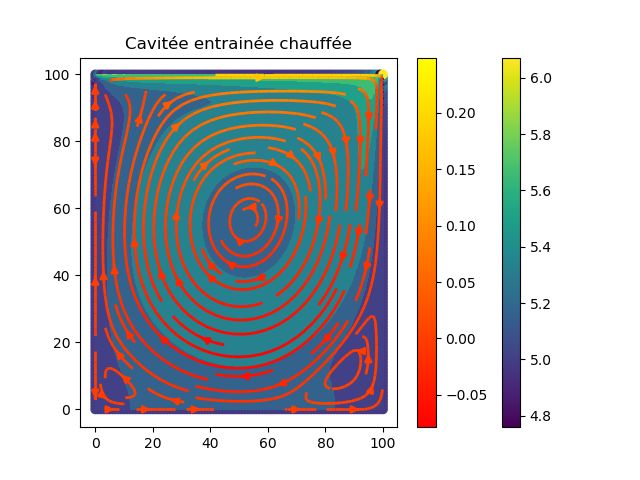
Équations de conservation et modèles de diffusion. Cette partie concerne l’étude des équations aux dérivées partielles du type Stokes, Navier Stokes, diffusion, diffusion anormale ou diffusion dans les milieux poreux, et de leurs formes dégénérées. Elle recquiert des connaissances solides en analyse fonctionnelle (espaces de Sobolev, formulation faible, résultats d’existence classiques pour les modèles elliptiques, paraboliques, hyperboliques). Par ailleurs, les approches récentes privilégiant les formulations par descente de gradients géométriques demandent également de maîtriser les outils de base de la géométrie différentielle et riemannienne et du transport optimal (espace de Wasserstein).
-
Description de l’aléa et analyse statistique. On s’intéresse aux modèles de marches aléatoires, de mouvements browniens et de martingales (en relation avec les problématiques évoquées dans le premier item). On s’intéresse également au traitement et à l’analyse de données, d’une part sous l’angle des statistiques (vraisemblance, inférence bayésienne, information de Fisher, géométrie de l’information) et d’autre part sous l’angle de la reconnaissance de formes et de l’apprentissage (méthodes de classification supervisée ou semi-supervisée, algorithmes de réduction de dimension) mais également et surtout du Deep Learning.
-
Méthodes numériques. L’objectif est de maîtriser des méthodes classiques (éléments finis, mise en oeuvre dans des cas simples, éléments finis d’ordre supérieur, Hermite, formulations mixtes, problèmes non linéaires, implémentation FreeFem++), et de s’initier aux méthodes des volumes finis et des réseaux lattice Boltzmann.
-
Traitement et analyse du signal et des images. L’acquisition d’information nécessite de fortes compétences en traitement du signal et des images. Cela passe par une bonne maîtrise des différents modes d’acquisition impliqués, une connaissance approfondies des méthodes récentes d’analyse et de traitement en lien avec les aspects multiéchelles. On s'intéresse en particulier aux diverses représentations utilisant les techniques hilbertiennes (transformées de Fourier, transformées en ondelettes et en curvelettes).
-
Modèles couplés (de tranfert et d’interfaces) : de l’expérimentation à la modélisation. Rares sont les phénomènes (naturels ou expérimentaux) qui se développent indépendamment de leur environnement : solutés et solvant, air et ballon, océan et trait de côte... On s’intéresse ici au couplage des interactions à différentes échelles et aux outils mathématiques pour traiter les non linéarités : points fixes, discrétisation, conditions aux bords.
Les savoir-faire
- Appréhender une problématique en termes d’ingénierie. Il s’agit d’être capable d’interagir avec des scientifiques d’autres disciplines et des interlocuteurs industriels pour définir un projet à partir d’une question concrète et lui apporter une réponse concrète (savoir-faire développé par les stages et les semaines Mathématiques et Entreprises).
- Exploiter les données sources. Un diplômé MIX doit être capable de traiter et d’analyser des données, de les confronter aux modèles existants et de faire évoluer ces modèles. Les solutions proposées doivent être implémentables efficacement. De l’optimisation de toutes ces démarches en fonction des contraintes et de la précision demandée résulte la réponse effective.
- Représenter et visualiser l’information. Cette partie concerne la représentation des phénomènes étudiés à partir des données acquises (traitées et analysées) et/ou des modèles mathématiques. La compétence recherchée est de rendre cette représentation la plus visuelle possible par des algorithmes de reconnaissance de formes, de synthèse de milieux ou de visualisation de champs de vitesse par exemple.
- Simuler les processus. Les phénomènes d’évolution sont simulés à partir de données expérimentales en prenant en compte l’influence des nombreux paramètres impliqués. Ces simulations doivent être efficaces en temps et en termes de ressources informatiques.
- Valider et restituer l’information. La maîtrise de l’ensemble de la démarche permet d’avoir un regard critique sur les simulations. C’est par conséquent un gage de la qualité et de la fiabilité des réponses qui seront apportées en contexte industriel.
Nos partenaires
ALSTOM, THALES, BULL-ATOS, NVDIA, SAFRAN-AIRBUS, BP-INEOS, BOWEN, IKOMIA, FARM PLUS, CRÉOCÉAN, TENSYL, DICARTECH, CASPEO, UNIMA, ECM, B<>COM, SEE-D, MADINTEC, Fédération Française de Backgammon, EXPERT- SOLUTIONS, IRTSNA, NUMTECH, VRAI + LOCAL, IRSSN, INRIA, INSERM, INRAE, CREATIS, LYRIC, GRETHA…
Le devenir des diplômés
Quelques exemples :
- Thèse CIFRE Agence Innovation Défense et BOWEN puis ingénieur de recherche INEO, Sophia Antipolis (Traitement du signal radar et intelligence artificielle)
- Ingénieur de recherche IKOMIA, La Rochelle (Intelligence artificielle)
- Thèse Université de Montpellier (Traitement des images satellitaires et intelligence artificielle)
- Thèse CIFRE, TENSYL, La Rochelle (Modèles de transition de phase pour les matériaux)
- Thèse École Navale de Brest (Traitement du signal sur les graphes)
- Thèse École Polytechnique, Palaiseau (Diffusion dans les milieux complexes)
- Ingénieur de recherche, université de La Rochelle (Intelligence artificielle)
- Thèse IRISA, Rennes (Intelligence artificielle et écriture manuscrite)
- Thèse CIFRE Thales (Traitement du signal)
- Thèse Université de Bordeaux (Intelligence artificielle et viniculture)
- Thèses Université de La Rochelle (Intelligence artificielle et algèbre géométrique, et simulations pour les écoulements dans les aquifères)
- Thèse CIFRE ORANGE (Optimisation de réseaux)
- Thèse ISM Aix-Marseille (Apprentissage visuel bio-inspiré)
- Thèse INRIA Bordeaux (Calcul Hautes Performances)
- Thèse INRIA Sophia Antipolis (IA, Modélisation numérique et biophysique)
- Thèse Institut polytechnique de Paris (IA Multimodale en temps réel)
- Ingénieur d’étude, LIENSs, Université de La Rochelle (Géophysique)
- Ingénieur d’étude, LEGOS, Université de Toulouse (Géophysique)
- Thèse Université de Grenoble (Traitement du signal bivarié)
Métiers et secteurs d'activité
- Ingénieur d'étude et de recherche (R et D)
- Ingénieur et cadre des méthodes de production et de contrôle
- Poursuite d'études en doctorat
- Secteurs industriels : technologie, télécommunication, aéronautique et spatial, pétrole, matériaux, mécanique, armement et défense...
- Secteur médical : imagerie, ingénierie des données, big data...
- Services : ressources environnementales, gestion des déchets et des pollutions, gestion des changements climatiques...
Champs de compétences stratégiques
- Intelligence Artificielle (IA) et Machine Learning (ML)
- MSO : Modélisation - Simulation - Optimisation
- Traitement du signal et des images