| Extravasation | Formation des complexes |
|---|---|
 |
 |
Objectif : Modéliser et simuler l'évolution des anticorps dans un cancer du côlon dans le cadre de l'immunothérapie, de l'injection à la destruction du cancer.
Le stage a eu lieu au sein de l'équipe MONC (Modélisation pour l'ONCologie), de l'INRIA. Le sujet proposé concernait l'application de l'immunothérapie dans le cas du cancer du côlon.
Méthodologie : utilisation des équations aux dérivées partielles et des éléments finis
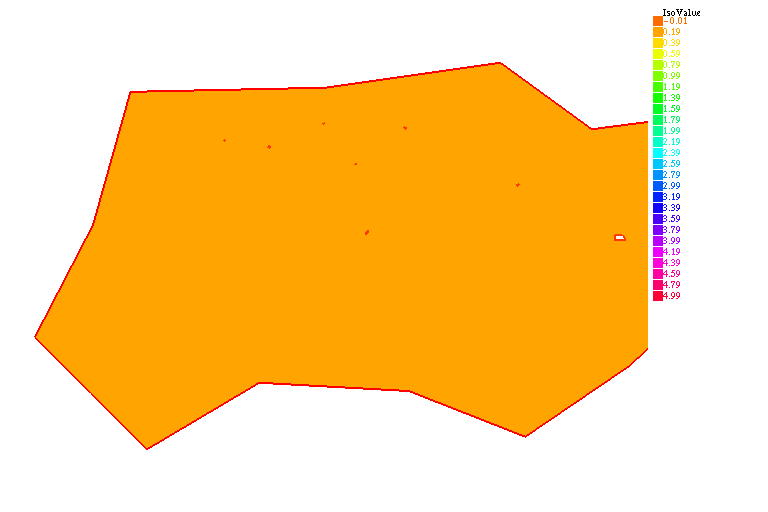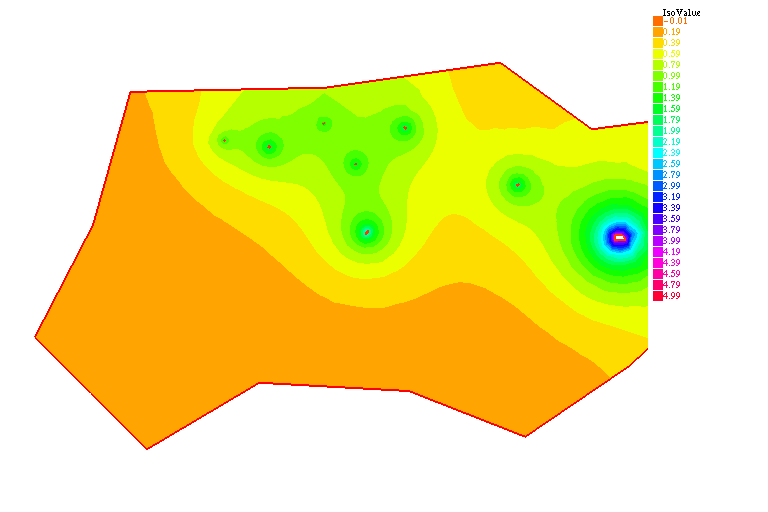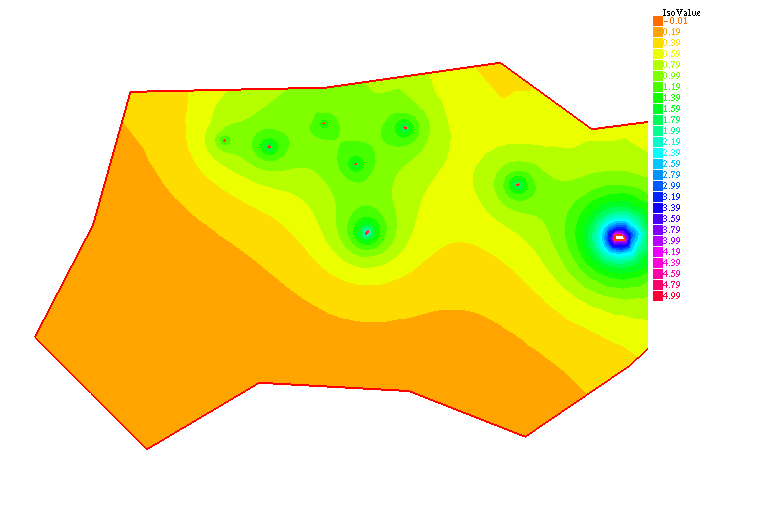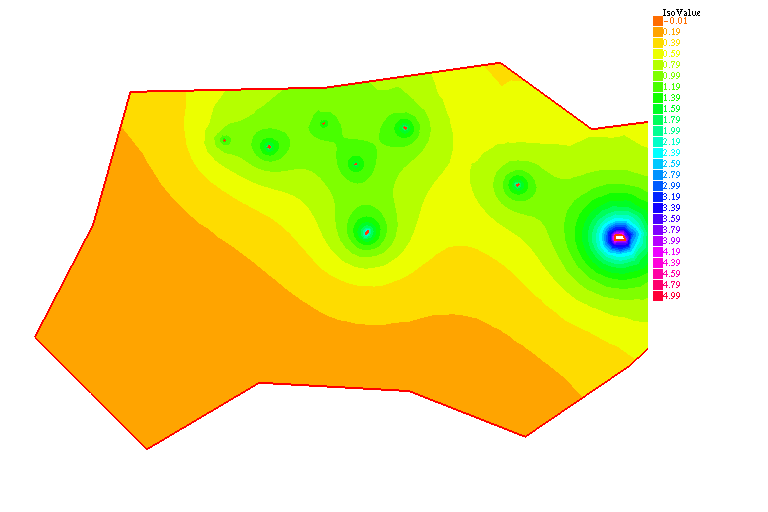
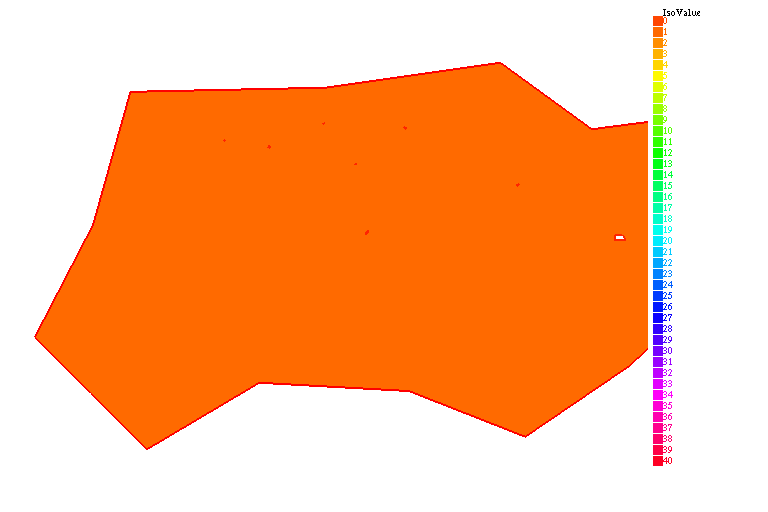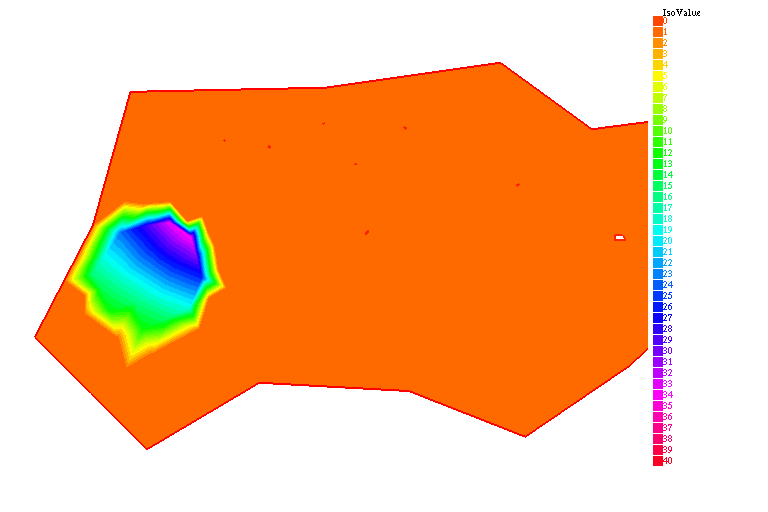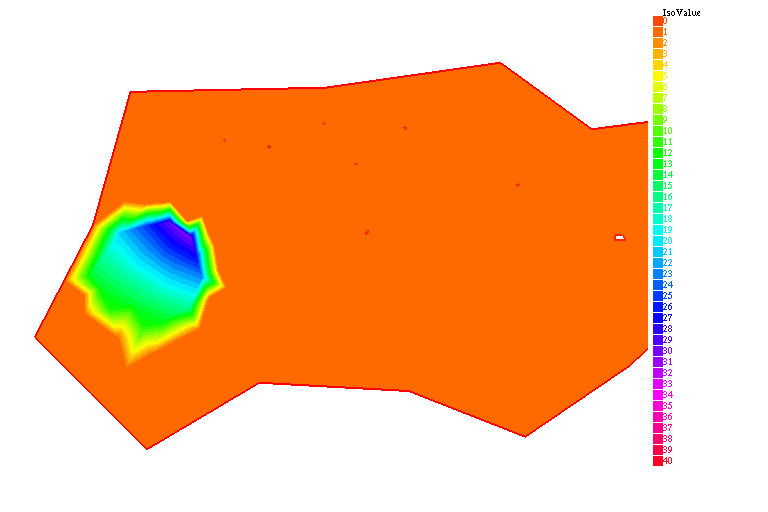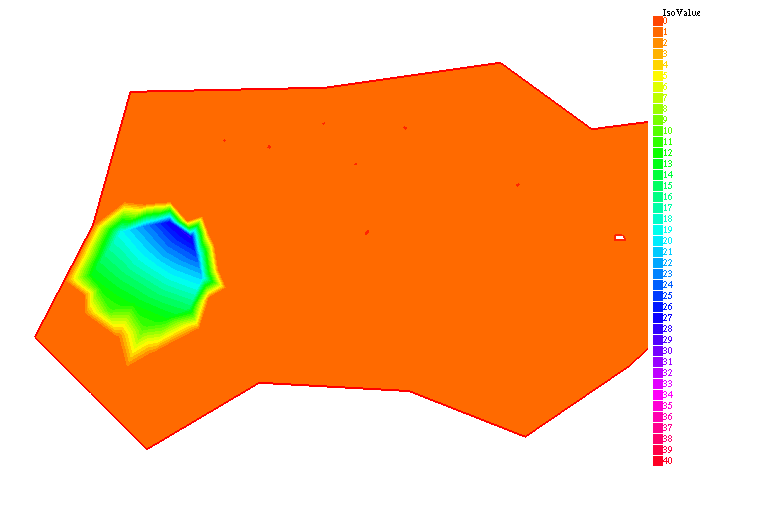
À partir de l'injection, l'évolution des anticorps se fait en quatre étapes :
- Les échanges entre les vaisseaux sanguins et la tumeur ($\nabla u_1\cdot n {|$)}
- La diffusion des anticorps libres ($u_1$) dans la tumeur
- La réaction entre les anticorps libres et les antigènes ($v$)
- La métabolisation des complexes anticorps-antigènes ($u_2$)
$$\frac{\partial u_1}{\partial t} = D\Delta u_1 - \frac{1}{\epsilon} k_1 u_1 v + k_2 u_2$$
$$\frac{\partial u_2}{\partial t} = \frac{1}{\epsilon}k_1 u_1 v - (k_2 + k_e) u_2$$
$$u_3 = u_3^0 (Ae^{-k_\alpha t} + Be^{-k_\beta t})$$
\begin{equation} \begin{split} \nabla u_1\cdot n {|\right) \ \nabla u_1\cdot n }} &= \frac{P}{D}\left(u_3 - \frac{u_1}{\epsilon{| &= 0 \end{split} \end{equation}} $$v + u_2 = 150$$
On remarque les échanges entre anticorps libres et complexes dans la première et la deuxième équation; le terme $-k_e u_2$ correspond à la métabolisation. On a une condition aux limites de Dirichlet homogène, une concentration d'anticorps dans le sang $u_3$ et la dernière équation donne la concentration d'antigènes $v$ dans le FAP, la seule partie de la tumeur les contenant. Les complexes ne peuvent donc se former que dans le FAP.
Ci-dessous, le transfert des anticorps des vaisseaux sanguins vers la tumeur, l'extravasation, et la formation des complexes.
| Extravasation | Formation des complexes |
|---|---|
 |
 |
Minimisation de la concentration de cellules tumorales
On cherche maintenant à minimiser la concentration de cellules tumorales tout au long de la simulation. Étant donné la fonction d'entrée $u_3 = u_3^0 (Ae^{-k_\alpha t} + Be^{-k_\beta t})$, nous allons tenter de trouver pour quelles valeurs de $k_\alpha$ et $k_\beta$ la concentration de cellules tumorales est minimale. La méthode utilisée sera l'algorithme de Metropolis, un algorithme stochastique qui a pour avantage de détecter efficacement les minimums globaux.
Par exemple, sur cette fonction de deux variables à trois minimums dont un unique global, on obtient :
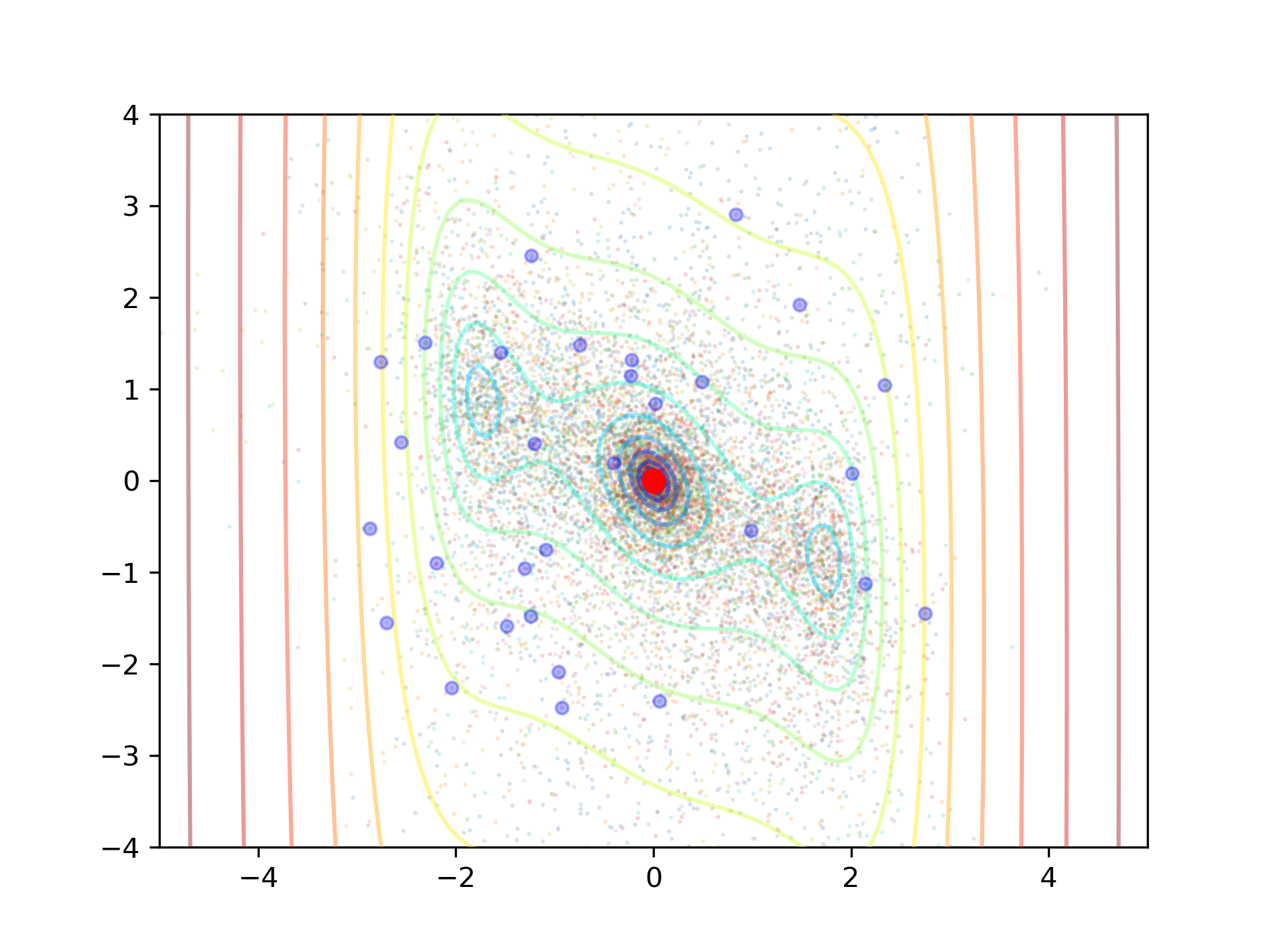
Les points de départ sont en bleu et les points d'arrivée en rouge.
En appliquant cette méthode à une fonction coût dépendant de la concentration de cellules tumorales en fonction de $k_\alpha$ et $k_\beta$, on obtient :
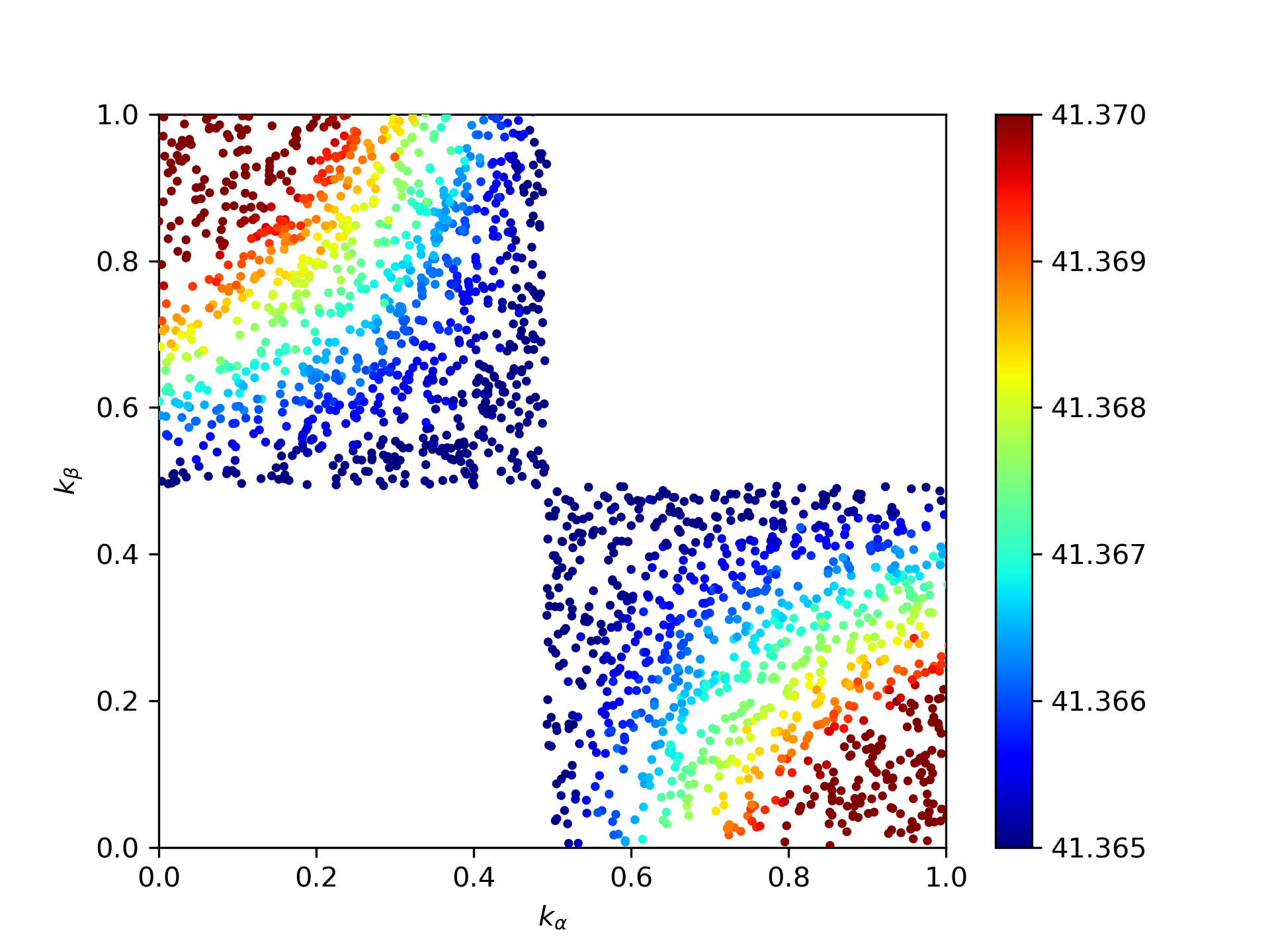
Un changement d'échelle a été fait en divisant les deux paramètres par $2\times 6.9\times 10^{-6}$. La concentration de cellules tumorales semble donc être minimale pour $k_\alpha = k_\beta = 6.9\times 10^{-6}$, ce qui est confirmé par le calcul.